ROBERTO FESTA

E

RICCARDO VARVERI

È noto che i concetti di benevolenza e amicizia hanno un ruolo fondamentale nel pensiero etico-politico di David Hume. Molto meno noto è il fatto che Hume è stato il primo a comprendere il carattere strategico delle relazioni sociali e politiche, al punto che viene oggi considerato da alcuni studiosi come un precursore della teoria dei giochi. Nelle pagine che seguono, mostreremo che questi due aspetti della riflessione humiana sono meno distanti di quanto sembri. Anzitutto, preciseremo la tesi che Hume è un proto-teorico dei giochi. Forniremo poi una breve illustrazione dei problemi di azione collettiva e del dilemma del prigioniero. Infine, mostreremo che un’adeguata formalizzazione della nozione humiana di benevolenza può essere applicata nella soluzione del dilemma del prigioniero.

David Hume come proto-teorico dei giochi.

Ogni giorno prendo decisioni di vario genere. Prima di uscire di casa, decido se portare l’ombrello. Dopo una forte nevicata, decido se aiutare il mio condomino a spalare la neve dalla porta del suo garage, nella speranza che ricambi il favore. Mentre la prima decisione riguarda solo me, la seconda dipende anche dalle mie attese circa le azioni del mio condomino. Questo significa che io e lui siamo coinvolti in un gioco, cioè in un’interazione strategica che coinvolge due o più individui, ciascuno dei quali agisce sulla base di ciò che si attende facciano gli altri. L’analisi sistematica delle interazioni strategiche viene intrapresa nell’ambito della teoria dei giochi, sviluppata a partire da Theory of Games and Economic Behavior (1944), di John von Neumann e Oskar Morgenstern. Alla fine degli anni Cinquanta, la teoria dei giochi fece il suo ingresso nelle scienze sociali. Questa circostanza favorì un rinnovato interesse per il pensiero di David Hume (1711-1776), che cominciò a essere visto come un precursore della teoria dei giochi. Nella sua affascinante interpretazione “giochistica” del pensiero etico-politico di Hume, Russell Hardin (David Hume: Moral and Political Theorist, 2007) sostiene che

Hume è un proto-teorico dei giochi, o almeno un pensatore strategico molto chiaro. […] Hume può essere letto come un filosofo politico della fine del XX secolo. Infatti, fino a tempi molto recenti solo Hume aveva tracciato una mappa praticamente completa delle più importanti interazioni sociali e politiche. […] Hume è un proto-scienziato sociale. Molte delle sue argomentazioni sono state successivamente avanzate da sociologi, politologi, psicologi ed economisti. È un precursore di Adam Smith in economia; di John von Neumann, Oskar Morgenstern e Thomas Schelling nella teoria dei giochi; di Robert Merton in sociologia; di Friedrich Hayek e degli Austriaci nella teoria politica e sociale; di David Lewis in filosofia; e di un gran numero di psicologi.

Anche Ken Binmore (David Hume: Grandfather of Modern Economics?, 2011) accredita a Hume l’anticipazione di molte idee della teoria dei giochi, come il concetto di equilibrio, introdotto da John Nash (premio Nobel nel 1994) e la teoria dei giochi ripetuti di Robert Aumann (premio Nobel nel 2005). Inoltre, secondo Binmore, Hume precorre l’approccio giochistico alle scienze economico-sociali, poiché anticipa la teoria del confronto interpersonale dell’utilità di John Harsanyi (premio Nobel nel 1994), l’economia sperimentale di Vernon Smith e l’economia comportamentale di Daniel Kahneman (premi Nobel nel 2002). Infine, Hume avrebbe anticipato la teoria delle convenzioni di Thomas Schelling (premio Nobel nel 2006) e le ricerche di Elinor Ostrom (premio Nobel nel 2009) sui meccanismi istituzionali per monitorare l’uso delle risorse naturali.

Problemi di azione collettiva e dilemma del prigioniero.

Un problema di azione collettiva è una situazione in cui tutti i membri di un gruppo sanno che il loro comune obiettivo sarà raggiunto se tutti coopereranno, ma ciascuno di loro sa anche che otterrà un risultato migliore se non coopererà. Problemi di questo genere vengono spesso etichettati come dilemmi sociali, con riferimento alla circostanza che la cooperazione tra i membri del gruppo è necessaria per raggiungere l’obiettivo condiviso da tutti loro, ma appare impossibile. Un compito fondamentale delle scienze sociali è quello di stabilire se, e come, i dilemmi sociali possano essere affrontati con successo mediante la cooperazione volontaria, oppure se la necessaria cooperazione possa essere ottenuta solo ricorrendo alla coercizione.

Molti problemi di azione collettiva sono stati visti come casi particolari del dilemma del prigioniero (DP), un gioco che deve il suo nome alla storiella con cui venne inizialmente illustrato, nel 1950, dal matematico canadese Albert Tucker. Un interessante caso di DP è lo scambio a distanza, illustrato dal seguente esempio.

I collezionisti Tizio e Caio scoprono su un forum online di possedere entrambi un doppione di un pezzo che manca all’altro e si accordano per scambiarsi i doppioni per posta. Entrambi devono decidere se rispettare l’accordo, spedendo il doppione al collega, oppure no. Si dice che un giocatore coopera (C) se spedisce il doppione e defeziona (D) se non lo spedisce. Il gioco ha quattro possibili risultati, ciascuno dei quali consiste nella combinazione delle azioni di Tizio e Caio. La mutua cooperazione e la mutua defezione vengono indicate, rispettivamente, con (C, C) e (D, D), il caso in cui Tizio coopera e Caio defeziona con (C, D) e quello in cui Tizio defeziona e Caio coopera con (D, C).

Nella versione classica della teoria dei giochi, formulata da von Neumann e Morgenstern, si presuppone che i giocatori siano egoisti, cioè che le preferenze di un giocatore tra i risultati del gioco siano determinate solo dai suoi guadagni nei diversi risultati. Si presuppone, inoltre, che i giocatori siano razionali, cioè che un giocatore rappresenti le sue preferenze con un’appropriata misura di utilità e scelga l’azione che massimizza la sua utilità. Nello scambio a distanza, l’utilità che Tizio e Caio attribuiranno a un risultato del gioco dipende dal valore assegnato ai pezzi mancanti e ai doppioni. Supponiamo, per esempio, che entrambi assegnino valore 2 a un pezzo mancante e valore 1 a un doppione. Allora, l’utilità attribuita da Tizio al risultato (C, C) sarà 1, poiché con questo risultato Tizio acquisisce un pezzo mancante di valore 2 e cede un doppione di valore 1. Analogamente, Tizio attribuirà utilità −1 a (C, D), utilità 2 a (D, C) e utilità 0 a (D, D). Le utilità di Caio verranno determinate nello stesso modo.

Nella matrice nella Figura 1, le possibili azioni di Tizio sono rappresentate dalle righe C e D e quelle di Caio dalle colonne C e D. Le quattro celle rappresentano i possibili risultati del gioco. In ciascuna di queste, il numero in basso a sinistra indica l’utilità attribuita da Tizio a quel risultato, mentre il numero in alto a destra indica quella attribuita da Caio.

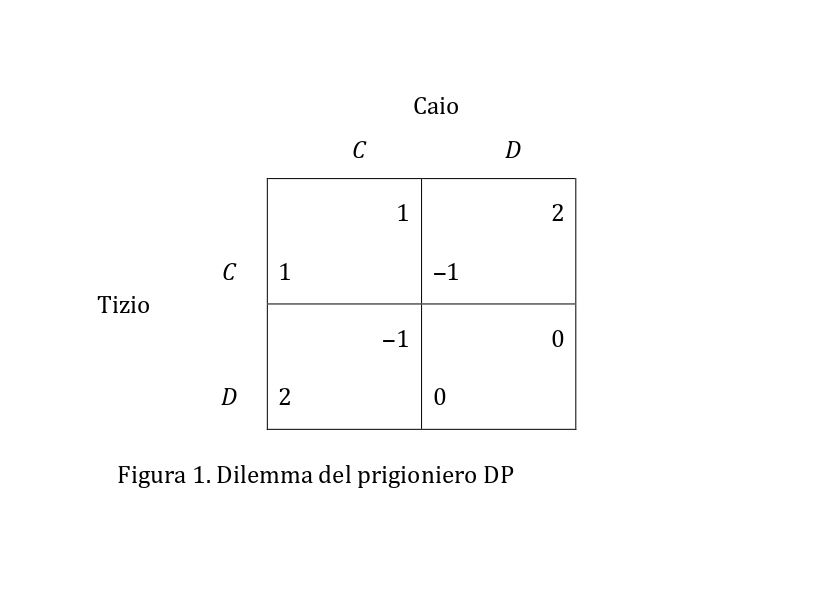
Poiché Tizio è razionale, comprende che la defezione domina la cooperazione, nel senso che, quale che sia l’azione di Caio, Tizio ottiene un’utilità più elevata se defeziona. Quindi, si può stare certi che Tizio defezionerà. Ovviamente, Caio deciderà nello stesso modo. Ciò significa che defezioneranno entrambi, cosicché non vi sarà alcuno scambio a distanza.

Il DP qui illustrato è un esempio canonico di dilemma sociale. Infatti, Tizio e Caio sanno che il loro obiettivo può essere raggiunto solo con la mutua cooperazione (C, C), ma ciascuno di loro sa anche che otterrà un risultato migliore defezionando. Pertanto, entrambi sceglieranno di defezionare, provocando così il disastro collettivo (D, D).

Fortunatamente, nelle interazioni sociali, i disastri collettivi previsti dalla teoria classica dei giochi si verificano di rado. Al contrario, come è stato documentato da una gran quantità di ricerche empiriche, gli individui alle prese con varie specie di DP manifestano una spiccata tendenza alla cooperazione. Questa circostanza suggerisce che gli esseri umani in carne e ossa sono diversi dagli egoisti razionali presupposti dalla teoria classica. Per esempio, potrebbero non essere totalmente egoisti. Si vedrà ora che David Hume considerò attentamente questa possibilità, formulando l’ipotesi dell’altruismo e applicandola nell’analisi delle interazioni sociali.

Simpatia, benevolenza e amicizia.

La nozione di simpatia (sympathy) svolge un ruolo fondamentale nel pensiero etico-politico di Hume.

Nessuna qualità della natura umana è più notevole, sia in sé sia nelle sue conseguenze, dell’attitudine che abbiamo a simpatizzare con gli altri, ricevendo attraverso la comunicazione le loro inclinazioni e sentimenti. […] Il piacere di un estraneo, a cui non siamo legati da alcuna amicizia, ci aggrada soltanto per simpatia. (Trattato sulla natura umana, 1739)

Hume usa “sympathy” in un’accezione più ampia di quella dell’inglese corrente, dove significa compassione, cioè partecipazione alla sofferenza altrui. Infatti, il termine humiano indica la partecipazione a qualunque emozione altrui. Hume vede la simpatia come una sorta di contagio emotivo, attraverso il quale le emozioni si trasmettono da una persona a un’altra. In determinate condizioni, la simpatia per una persona suscita un sentimento di benevolenza nei suoi confronti, che si manifesta nel provare piacere per il suo piacere.

Hume ritiene che si possa provare simpatia e benevolenza per qualunque essere umano, compresi gli estranei. In contrasto con la concezione tradizionale, secondo la quale gli uomini sono egoisti per natura, Hume ritiene che la benevolenza non sia un travestimento dell’egoismo, bensì una disposizione profondamente radicata nella natura umana.

Gli animali sono capaci di mostrare benevolenza tanto nei riguardi della loro stessa specie quanto nei nostri riguardi, né c’è, in questo caso, il minimo sospetto di dissimulazione o di artificio. […] [S]e ammettiamo una benevolenza disinteressata nelle specie inferiori, con quale regola di analogia potremo rifiutarla alla specie superiore? […] Questi e mille altri casi sono segni d’una generale benevolenza nella natura umana. […] L’ipotesi che ammette una benevolenza disinteressata, distinta dall’amore di sé, ha realmente in sé maggiore semplicità ed è più conforme all’analogia di natura di quella che pretende di risolvere ogni sentimento di amicizia e di umanità nell’amore di sé. […] Dov’è la difficoltà nel concepire […] che, per l’originaria struttura del nostro temperamento, potremmo sentire un desiderio della felicità o bene degli altri, il quale, per mezzo di questa passione, diventerebbe il nostro stesso bene e verrebbe in seguito ricercato, in base ai moventi combinati della benevolenza e del piacere personale? […] Non si può porre in discussione senza la massima assurdità […] che c’è un po’ di benevolenza, per quanto poca, infusa nel nostro cuore, qualche scintilla di amicizia per la specie umana, qualche particella della colomba impastata nella nostra struttura, insieme con gli elementi del lupo e del serpente. (Ricerca sui principi della morale, 1751) (Corsivo aggiunto.)

La «generale benevolenza» degli esseri umani è una delle due specie di benevolenza suscitate dalla simpatia. L’altra specie, di gran lunga più intensa, è la «benevolenza particolare», che «si fonda sopra un’opinione circa la virtù della persona, su dei servigi resici o su alcune particolari relazioni» (ibid.). L’oggetto della benevolenza particolare sono i nostri amici, intesi come le persone che, per varie ragioni, amiamo. Hume non esita ad affermare che

l’amicizia è la principale gioia della vita umana. (Ricerca sull’intelletto umano,1748).

Sull’intensità della benevolenza verso gli amici, Hume si esprime così.

Se anche tutte le forze e gli elementi naturali si organizzassero per servire e obbedire a un solo uomo; se anche il sole sorgesse e calasse al suo comando; se il mare e i fiumi scorressero a suo piacimento, e la terra fornisse spontaneamente tutto quel che gli potesse essere utile o gradevole; egli rimarrebbe pur sempre un miserabile, fino a che non [gli si desse] almeno una persona con cui condividere la sua felicità, e della cui stima e amicizia poter godere. […] La benevolenza, ossia l’appetito che accompagna l’amore, è un desiderio per la felicità della persona amata, e un’avversione per la sua miseria. (Trattato sulla natura umana, 1739). [Corsivo aggiunto.]

Giochi di altruismo. Una soluzione humiana del dilemma del prigioniero.

Sebbene negli scritti di Hume non compaia il termine “altruismo”, che fu coniato solo nel 1851 da Auguste Comte, non vi è alcuna sostanziale differenza tra l’altruismo e la benevolenza humiana. Non esiteremo, quindi, a parlare di ipotesi dell’altruismo per indicare l’ipotesi humiana secondo la quale, nella maggior parte degli esseri umani, l’egoismo convive con una certa dose di benevolenza.

Nell’articolo Beyond Sympathy and Empathy (2022), Robert Sugden osserva che nella teoria della scelta razionale, di cui fa parte la teoria dei giochi, il comportamento non egoistico può essere spiegato in termini di preferenze.

Il modo più ovvio per rappresentare la motivazione non egoistica è vederla come una specie di preferenza. Da qui l’idea, ormai consolidata nella teoria della scelta razionale, di assumere quelle che sono variamente chiamate preferenze altruistiche, benevole o simpatetiche: Joe è simpatetico con Jane nella misura in cui […] [preferisce] che le preferenze di Jane siano soddisfatte.

 Una delle prime applicazioni delle preferenze altruistiche nell’analisi delle interazioni sociali si deve a Michael C. Taylor (The Possibility of Cooperation, 1987), che attribuisce a Hume il merito di avere intuito che, in molte interazioni sociali, gli individui si comportano come altruisti razionali, cioè come individui razionali mossi da motivazioni (almeno in parte) altruistiche:

Hume parte dal presupposto che la maggior parte delle persone si preoccupa principalmente dei propri guadagni, ma possiede anche una limitata quantità di benevolenza.

Taylor mostra che un’adeguata formalizzazione dell’ipotesi humiana dell’altruismo può spiegare la diffusa tendenza alla cooperazione in DP e negli altri dilemmi sociali. Senza addentrarci nei dettagli matematici della sua analisi, qui sotto ne illustriamo un’idea chiave.

Come si ricorderà, il DP in Figura 1 si fonda sul presupposto che Tizio e Caio hanno utilità egoistiche, nel senso che l’utilità attribuita da ciascuno di loro a un risultato del gioco dipende solo dal suo guadagno in quel risultato. D’altra parte, nulla vieta di supporre, in accordo con l’ipotesi humiana dell’altruismo, che le utilità di Tizio e Caio siano utilità altruistiche, cioè che l’utilità attribuita da ciascuno di loro a un risultato del gioco dipenda sia dal suo guadagno in quel risultato sia da quello del collega. È proprio questa la supposizione fatta da Taylor, che introduce la seguente classe di utilità humiane.

Date le utilità egoistiche u(T) e u(C) attribuite da Tizio e Caio a un determinato risultato del DP in Figura 1, l’utilità humiana h(T) che Tizio assegna a quel risultato è la media ponderata di u(T) e u(C):

(1) h(T) ≡ αu(T) + βu(C) dove α, β ≥ 0 e α + β = 1.

Il carattere altruistico di h(T) consiste nel fatto che h(T) è positivamente influenzata non solo dall’utilità egoistica u(T) di Tizio, ma anche dall’utilità egoistica u(C) di Caio. I pesi α e β indicano, rispettivamente, l’intensità dell’egoismo e dell’altruismo di Tizio. Pertanto, le quantità αu(T) e βu(C) possono venire intese come misure, rispettivamente, del piacere egoistico u(T) di Tizio e del suo piacere altruistico, provato lasciandosi contagiare dal piacere egoistico u(C) di Caio. L’utilità humiana h(C) di Caio verrà definita sulla falsariga di (1): h(C) ≡ αu(C) + βu(T).

Le definizioni di h(T) e h(C) permettono di determinare le utilità humiane di Tizio e Caio nei quattro risultati del DP in Figura 1. Supponiamo, per esempio, che α = 0,6 e β = 0,4. Allora, nel risultato (C, C), le utilità humiane saranno h(T) = h(C) = 1, in (D, D), saranno h(T) = h(C) = 0; in (C, D), saranno h(T) = 0,2 e h(C) = 0,8; infine, in (D, C), saranno h(T) = 0,8 e h(C) = 0,2.

Sostituendo le utilità egoistiche u(T) e u(C) nel DP in Figura 1 con le utilità humiane h(T) e h(C), si ottiene il trasformato humiano HDP di DP, raffigurato in Figura 2.

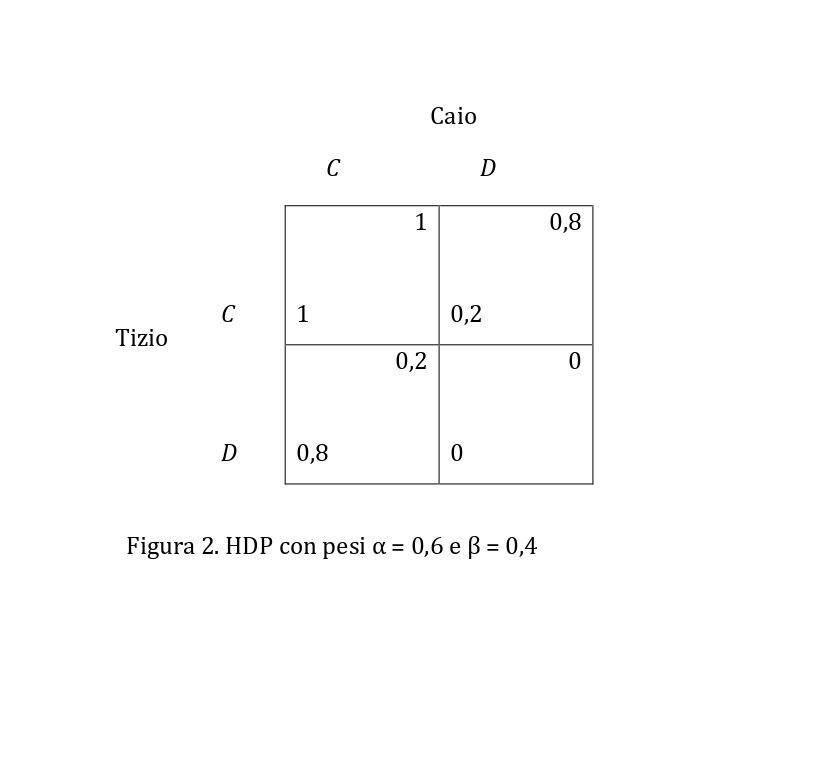
Si può notare che HDP è un gioco molto diverso da DP, poiché in HDP la cooperazione domina la defezione. Infatti, Tizio comprende che, quale che sia l’azione di Caio, otterrà un’utilità più elevata se coopera. Ovviamente, Caio arriverà alla stessa conclusione. Quindi, Tizio e Caio coopereranno entrambi, evitando il disastro collettivo (D, D) e ottenendo l’utilità 1 della mutua cooperazione (C, C). Ciò significa che HDP non è un dilemma del prigioniero. Si può dimostrare che basta che i due giocatori condividano un modesto indice di altruismo (β > 1/3) per trasformare il DP in Figura 1 in un gioco HDP in cui domina la cooperazione.

Il caso qui illustrato suggerisce che le tendenze cooperative nei dilemmi del prigioniero possono venire spiegate con l’altruismo dei partecipanti. Più precisamente, si può ipotizzare che due altruisti razionali tenderanno trasformare le utilità del loro DP nelle corrispondenti utilità humiane. In tal modo si affronteranno nel trasformato humiano HDP di DP, cioè in un gioco dove, con un modesto indice altruismo, dominerà la cooperazione.

ENDOXA - BIMESTRALE FILOSOFIA ENDOXA SETTEMBRE 2024 POLITICHE DELL'AMICIZIA/INIMICIZIA Riccardo Varveri Roberto Festa